《机器人与数字人:基于MATLAB的建模与控制》——2.1节向量、坐标变换和空间描述...
本文共 763 字,大约阅读时间需要 2 分钟。
本节书摘来自华章社区《机器人与数字人:基于MATLAB的建模与控制》一书中的第2章,第2.1节向量、坐标变换和空间描述,作者[美]顾友谅(Edward Y.L.Gu),更多章节内容可以访问云栖社区“华章社区”公众号查看
2.1向量、坐标变换和空间描述
一般情况下,一个向量可以有以下两种不同类型的定义:1点向量——向量仅由它的长度和方向确定,与它的终点位置无关。依据此定义,不管向量的终点位于何处,任意两个长度和符号相同的平行向量相等。为了表示这种类型的向量,通常把终点放置在参考系的原点并用箭头指出方向,坐标值的增加量就构成了点向量。2线向量——向量不仅由它的长度和方向确定,也取决于它的位置。因此,两个不同直线的平行向量,即使有相同长度和符号也被认为是不相等的向量。直观地看,为了准确定义这种线向量,图2-1长度相同的两个平行向量必须定义两个独立的点向量,其中一个定义它的长度和方向,另一个确定它的终点位置或者所在直线的“矩”。也就是说,线向量在三维空间应该具有6个分量。一个典型且有效的线向量的数学描述方法就是所谓的对偶代数[1],将在本章后面介绍。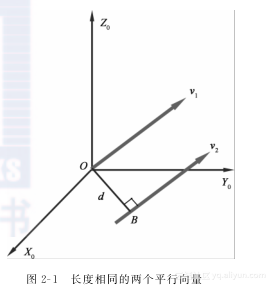
转载地址:http://gmaex.baihongyu.com/
你可能感兴趣的文章
Android笔记:通过RadioGroup/RadioButton自定义tabhost的简单方法
查看>>
ELCSlider
查看>>
XCode工程中 Targets详解
查看>>
Ext.Msg.prompt的高级应用
查看>>
Postgres 中 to_char 格式化记录
查看>>
关于联合索引
查看>>
开源 java CMS - FreeCMS2.7 登录移动端管理中心
查看>>
Android FM模块学习之三 FM手动调频
查看>>
Python 设置系统默认编码以及其他编码问题大全
查看>>
Vbs脚本编程简明教程之十四
查看>>
如何UDP/TCP端口是否通了
查看>>
pxe实现系统的自动化安装
查看>>
Redis高可用技术解决方案总结
查看>>
Scale Out Owncloud 高可用(2)
查看>>
何为敏捷
查看>>
HA集群之四:Corosync+Pacemaker+DRBD实现HA Mysql
查看>>
服务器定义
查看>>
我的友情链接
查看>>
分布式系统的面试题15
查看>>
个人代码库の创建快捷方式
查看>>